Consider Again the Ground State of the Harmonic Osillator. Find X^2

Quantum Mechanics

54 The Quantum Harmonic Oscillator

Learning Objectives

By the end of this section, you lot will be able to:

Describe the model of the quantum harmonic oscillator
Place differences between the classical and quantum models of the harmonic oscillator
Explain physical situations where the classical and the quantum models coincide

Oscillations are constitute throughout nature, in such things as electromagnetic waves, vibrating molecules, and the gentle dorsum-and-forth sway of a tree branch. In previous chapters, we used Newtonian mechanics to study macroscopic oscillations, such as a block on a spring and a uncomplicated pendulum. In this chapter, we begin to study oscillating systems using quantum mechanics. Nosotros begin with a review of the classic harmonic oscillator.

The Classic Harmonic Oscillator

A simple harmonic oscillator is a particle or system that undergoes harmonic motion about an equilibrium position, such every bit an object with mass vibrating on a spring. In this department, we consider oscillations in i-dimension only. Suppose a mass moves back-and-forth forth the

ten-direction most the equilibrium position, $x=0$ . In classical mechanics, the particle moves in response to a linear restoring force given by ${F}_{x}=\text{−}kx,$ where ten is the displacement of the particle from its equilibrium position. The motion takes identify between two turning points, $x=\text{±}A$ , where A denotes the amplitude of the motion. The position of the object varies periodically in time with athwart frequency $\omega =\sqrt{k\text{/}m},$ which depends on the mass m of the oscillator and on the forcefulness abiding k of the cyberspace force, and tin can be written every bit

$x\left(t\right)=A\phantom{\rule{0.2em}{0ex}}\text{cos}\text{ }\left(\omega \text{ }\text{ }t+\varphi \right).$

The total energy E of an oscillator is the sum of its kinetic energy $K=m{u}^{2}\text{/}2$ and the elastic potential energy of the force $U\left(x\right)=k\text{ }{x}^{2}\text{/}2,$

$E=\frac{1}{2}m{u}^{2}+\frac{1}{2}k{x}^{2}.$

At turning points $x=\text{±}A$ , the speed of the oscillator is zippo; therefore, at these points, the energy of oscillation is solely in the form of potential energy $E=k\text{ }{A}^{\text{ }2}\text{/}2$ . The plot of the potential free energy U(x) of the oscillator versus its position x is a parabola ((Figure)). The potential-free energy office is a quadratic function of x, measured with respect to the equilibrium position. On the same graph, nosotros also plot the total energy E of the oscillator, every bit a horizontal line that intercepts the parabola at $x=\text{±}A$ . Then the kinetic energy K is represented equally the vertical altitude between the line of total energy and the potential energy parabola.

The potential energy well of a classical harmonic oscillator: The motility is confined between turning points at $x=\text{−}A$ and at $x=+A$ . The energy of oscillations is $E=k{A}^{2}\text{/}2.$

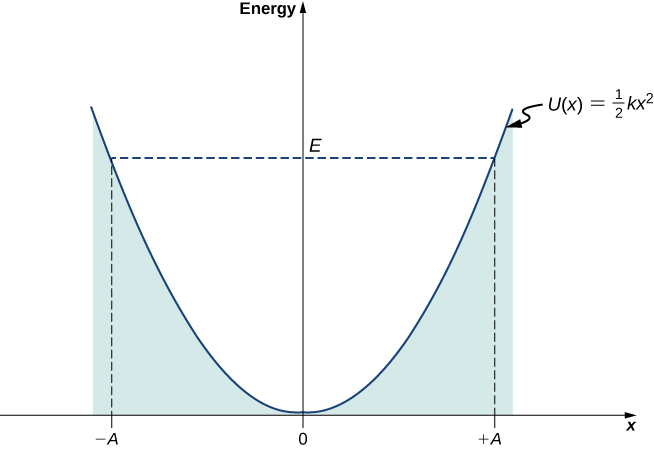
A graph of the potential U of x and energy E is shown. The vertical axis is energy and the horizontal axis is x. The energy E is positive and constant. The potential U of x is the function one half k times x squared, a concave up parabola whose value is zero at x=0. The region below the U of x curve is shaded. U of x is equal to E at x equal to minus A and x equal to plus A.

In this plot, the movement of a classical oscillator is confined to the region where its kinetic energy is nonnegative, which is what the energy relation (Effigy) says. Physically, it means that a classical oscillator can never exist plant beyond its turning points, and its energy depends just on how far the turning points are from its equilibrium position. The free energy of a classical oscillator changes in a continuous way. The lowest energy that a classical oscillator may take is zero, which corresponds to a situation where an object is at rest at its equilibrium position. The nil-free energy state of a classical oscillator but means no oscillations and no move at all (a classical particle sitting at the bottom of the potential well in (Figure)). When an object oscillates, no matter how big or pocket-size its energy may exist, it spends the longest time near the turning points, considering this is where it slows down and reverses its direction of motion. Therefore, the probability of finding a classical oscillator between the turning points is highest almost the turning points and lowest at the equilibrium position. (Annotation that this is not a statement of preference of the object to go to lower energy. It is a statement almost how quickly the object moves through various regions.)

The Quantum Harmonic Oscillator

1 problem with this classical formulation is that information technology is not general. We cannot use information technology, for instance, to describe vibrations of diatomic molecules, where quantum furnishings are important. A first step toward a breakthrough formulation is to use the classical expression $k=m\text{ }{\omega }^{\text{ }2}$ to limit mention of a "spring" constant between the atoms. In this way the potential energy role can exist written in a more than general form,

$U\left(x\right)=\frac{1}{2}m{\omega }^{\text{ }2}{x}^{\text{ }2}.$

Combining this expression with the time-contained Schrӧdinger equation gives

$-\frac{\hslash }{2m}\phantom{\rule{0.2em}{0ex}}\frac{{d}^{\text{ }2}\psi \left(x\right)}{d\text{ }{x}^{2}}+\frac{1}{2}m{\omega }^{\text{ }2}{x}^{\text{ }2}\psi \left(x\right)=E\psi \left(x\right).$

To solve (Figure)—that is, to find the allowed energies E and their respective wave functions $\psi \left(x\right)$ —we require the moving ridge functions to be symmetric about $x=0$ (the lesser of the potential well) and to be normalizable. These weather ensure that the probability density $|\psi \left(x\right){|}^{\text{ }2}$ must be finite when integrated over the entire range of 10 from $\text{−}\infty$ to $+\infty$ . How to solve (Figure) is the subject of a more than advanced course in breakthrough mechanics; hither, we simply cite the results. The immune energies are

${E}_{n}=\left(n+\frac{1}{2}\right)\hslash \omega =\frac{2n+1}{2}\hslash \omega ,\phantom{\rule{0.5em}{0ex}}n=0,1,2,3,...$

The wave functions that correspond to these energies (the stationary states or states of definite energy) are

${\psi }_{n}\left(x\right)={N}_{n}{e}^{\text{ }-{\beta }^{\text{ }2}{x}^{\text{ }2}\text{/}2}{H}_{n}\left(\beta x\right),\phantom{\rule{0.5em}{0ex}}n=0,1,2,3,...$

where $\beta =\sqrt{m\text{ }\text{ }\omega \text{/}\hslash }$ , ${N}_{n}$ is the normalization constant, and ${H}_{n}\left(y\right)$ is a polynomial of degree due north called a Hermite polynomial . The first four Hermite polynomials are

$\begin{array}{c}{H}_{0}\left(y\right)=1\hfill \\ {H}_{1}\left(y\right)=2y\hfill \\ {H}_{2}\left(y\right)=4{y}^{2}-2\hfill \\ {H}_{3}\left(y\right)=8{y}^{3}-12y.\hfill \end{array}$

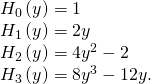
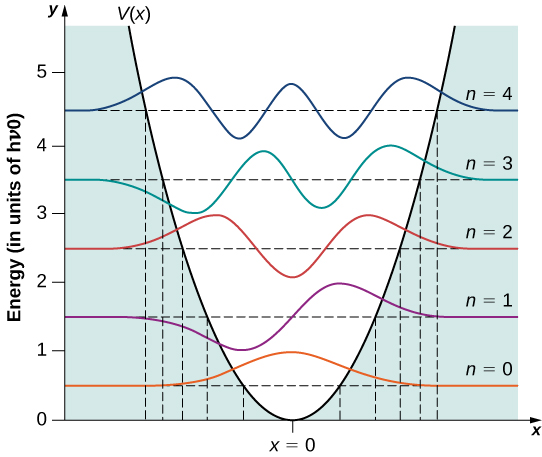
A few sample moving ridge functions are given in (Figure). As the value of the main number increases, the solutions alternate between even functions and odd functions near $x=0$ .

The get-go v moving ridge functions of the quantum harmonic oscillator. The classical limits of the oscillator'south motion are indicated by vertical lines, corresponding to the classical turning points at $x=\text{±}A$ of a classical particle with the same energy as the energy of a quantum oscillator in the state indicated in the effigy.

Classical Region of Harmonic Oscillations Find the aamplitude A of oscillations for a classical oscillator with free energy equal to the free energy of a quantum oscillator in the quantum state n.

Strategy To determine the aamplitude A, nosotros set the classical energy $E=k{x}^{2}\text{/}2=m\text{ }{\omega }^{2}{A}^{2}\text{/}2$ equal to ${E}_{n}$ given by (Figure).

Solution Nosotros obtain

${E}_{n}=m\text{ }{\omega }^{2}{A}_{n}^{\text{ }2}\text{/}2\phantom{\rule{0.5em}{0ex}}⇒\phantom{\rule{0.5em}{0ex}}{A}_{n}=\sqrt{\frac{2}{m\text{ }{\omega }^{\text{ }2}}{E}_{n}}=\sqrt{\frac{2}{m\text{ }{\omega }^{\text{ }2}}\phantom{\rule{0.2em}{0ex}}\frac{2n+1}{2}\hslash \omega }=\sqrt{\left(2n+1\right)\frac{\hslash }{m\text{ }\omega }}.$

Significance Equally the quantum number n increases, the energy of the oscillator and therefore the amplitude of oscillation increases (for a fixed natural angular frequency. For large n, the amplitude is approximately proportional to the foursquare root of the quantum number.

Several interesting features announced in this solution. Unlike a classical oscillator, the measured energies of a breakthrough oscillator can have just energy values given past (Effigy). Moreover, unlike the case for a quantum particle in a box, the allowable energy levels are evenly spaced,

$\text{Δ}E={E}_{n+1}-{E}_{n}=\frac{2\left(n+1\right)+1}{2}\hslash \omega -\frac{2n+1}{2}\hslash \omega =\hslash \omega =h\text{ }f.$

When a particle leap to such a system makes a transition from a higher-energy state to a lower-energy country, the smallest-energy quantum carried by the emitted photon is necessarily hf. Similarly, when the particle makes a transition from a lower-energy land to a college-energy state, the smallest-free energy breakthrough that tin can be absorbed by the particle is hf. A quantum oscillator tin absorb or emit energy just in multiples of this smallest-energy breakthrough. This is consistent with Planck'south hypothesis for the energy exchanges between radiation and the cavity walls in the blackbody radiations problem.

Vibrational Energies of the Hydrogen Chloride MoleculeThe HCl diatomic molecule consists of i chlorine atom and one hydrogen atom. Because the chlorine cantlet is 35 times more massive than the hydrogen atom, the vibrations of the HCl molecule tin can be quite well approximated by assuming that the Cl atom is motionless and the H cantlet performs harmonic oscillations due to an elastic molecular force modeled by Hooke's law. The infrared vibrational spectrum measured for hydrogen chloride has the lowest-frequency line centered at $f=8.88\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{ }13}\phantom{\rule{0.2em}{0ex}}\text{Hz}$ . What is the spacing between the vibrational energies of this molecule? What is the strength constant grand of the diminutive bail in the HCl molecule?

Strategy The lowest-frequency line corresponds to the emission of lowest-frequency photons. These photons are emitted when the molecule makes a transition between ii adjacent vibrational energy levels. Assuming that energy levels are equally spaced, nosotros use (Figure) to estimate the spacing. The molecule is well approximated by treating the Cl atom as existence infinitely heavy and the H cantlet as the mass g that performs the oscillations. Treating this molecular arrangement as a classical oscillator, the forcefulness constant is found from the classical relation $k=m\text{ }{\omega }^{\text{ }2}$ .

Solution The free energy spacing is

$\text{Δ}E=h\text{ }f=\left(4.14\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{ }-15}\text{eV}·\text{s}\right)\left(8.88\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{ }13}\phantom{\rule{0.2em}{0ex}}\text{Hz}\right)=0.368\phantom{\rule{0.2em}{0ex}}\text{eV}\text{.}$

The forcefulness abiding is

$k=m\text{ }{\omega }^{\text{ }2}=m\text{ }{\left(2\pi f\right)}^{2}=\left(1.67\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{ }-27}\phantom{\rule{0.2em}{0ex}}\text{kg}\right){\left(2\pi \phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}8.88\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{ }13}\phantom{\rule{0.2em}{0ex}}\text{Hz}\right)}^{2}=520\phantom{\rule{0.2em}{0ex}}\text{N}\text{/}\text{m}.$

Significance The forcefulness between atoms in an HCl molecule is surprisingly stiff. The typical energy released in energy transitions between vibrational levels is in the infrared range. As we will see later, transitions in between vibrational free energy levels of a diatomic molecule often back-trail transitions betwixt rotational energy levels.

Check Your Agreement The vibrational frequency of the hydrogen iodide How-do-you-do diatomic molecule is $6.69\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{ }13}\phantom{\rule{0.2em}{0ex}}\text{Hz}$ . (a) What is the force constant of the molecular bond between the hydrogen and the iodine atoms? (b) What is the energy of the emitted photon when this molecule makes a transition betwixt adjacent vibrational free energy levels?

a. 295 N/one thousand; b. 0.277 eV

The quantum oscillator differs from the classic oscillator in three means:

Outset, the ground state of a quantum oscillator is ${E}_{0}=\hslash \omega \text{/}2,$ not zero. In the classical view, the lowest energy is zero. The nonexistence of a cypher-energy state is mutual for all quantum-mechanical systems because of omnipresent fluctuations that are a consequence of the Heisenberg uncertainty principle. If a quantum particle sat motionless at the bottom of the potential well, its momentum also equally its position would take to be simultaneously verbal, which would violate the Heisenberg dubiousness principle. Therefore, the lowest-energy land must be characterized by uncertainties in momentum and in position, then the basis state of a quantum particle must prevarication above the bottom of the potential well.

2nd, a particle in a quantum harmonic oscillator potential tin be establish with nonzero probability exterior the interval $\text{−}A\le x\le +A$ . In a classic formulation of the trouble, the particle would not take any energy to be in this region. The probability of finding a ground-state quantum particle in the classically forbidden region is near 16%.

Third, the probability density distributions $|{\psi }_{n}\left(x\right){|}^{\text{ }2}$ for a quantum oscillator in the footing low-energy state, ${\psi }_{0}\left(x\right)$ , is largest at the heart of the well $\left(x=0\right)$ . For the particle to be found with greatest probability at the center of the well, nosotros wait that the particle spends the most time there as it oscillates. This is contrary to the beliefs of a classical oscillator, in which the particle spends near of its time moving with relative small speeds almost the turning points.

Check Your Understanding Find the expectation value of the position for a particle in the ground state of a harmonic oscillator using symmetry.

$〈x〉=0$

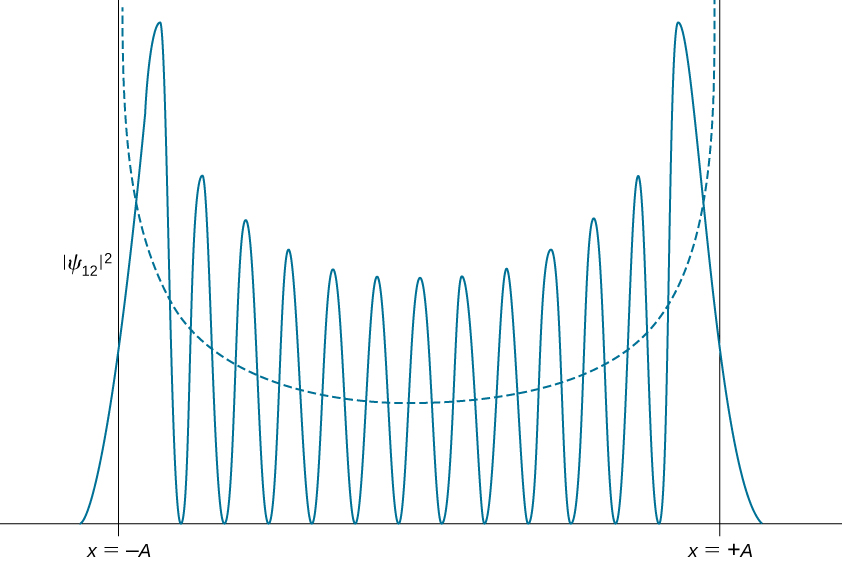
Quantum probability density distributions change in graphic symbol for excited states, condign more like the classical distribution when the quantum number gets college. We observe this change already for the first excited state of a quantum oscillator because the distribution $|{\psi }_{1}\left(x\right){|}^{\text{ }2}$ peaks up effectually the turning points and vanishes at the equilibrium position, as seen in (Effigy). In accordance with Bohr's correspondence principle, in the limit of high quantum numbers, the breakthrough description of a harmonic oscillator converges to the classical description, which is illustrated in (Figure). The classical probability density distribution corresponding to the breakthrough energy of the $n=12$ state is a reasonably good approximation of the breakthrough probability distribution for a quantum oscillator in this excited state. This agreement becomes increasingly improve for highly excited states.

The probability density distribution for finding the quantum harmonic oscillator in its $n=12$ quantum state. The dashed curve shows the probability density distribution of a classical oscillator with the same free energy.

Summary

The quantum harmonic oscillator is a model congenital in illustration with the model of a classical harmonic oscillator. Information technology models the behavior of many physical systems, such as molecular vibrations or wave packets in quantum eyes.
The immune energies of a quantum oscillator are discrete and evenly spaced. The energy spacing is equal to Planck's energy quantum.
The basis state energy is larger than null. This ways that, unlike a classical oscillator, a quantum oscillator is never at residue, fifty-fifty at the bottom of a potential well, and undergoes quantum fluctuations.
The stationary states (states of definite energy) take nonzero values too in regions beyond classical turning points. When in the footing land, a quantum oscillator is most likely to be constitute around the position of the minimum of the potential well, which is the least-probable position for a classical oscillator.
For loftier quantum numbers, the move of a quantum oscillator becomes more similar to the motion of a classical oscillator, in accordance with Bohr's correspondence principle.

Conceptual Questions

Is information technology possible to measure energy of $0.75\hslash \omega$ for a breakthrough harmonic oscillator? Why? Why not? Explain.

No. This energy corresponds to $n=0.25$ , but n must be an integer.

Explain the connection betwixt Planck's hypothesis of energy quanta and the energies of the quantum harmonic oscillator.

If a classical harmonic oscillator can exist at rest, why tin can the quantum harmonic oscillator never be at rest? Does this violate Bohr'due south correspondence principle?

Because the smallest allowed value of the quantum number n for a simple harmonic oscillator is 0. No, considering quantum mechanics and classical mechanics agree only in the limit of large $n$ .

Use an case of a quantum particle in a box or a quantum oscillator to explain the concrete meaning of Bohr'due south correspondence principle.

Can we simultaneously measure position and free energy of a quantum oscillator? Why? Why non?

Yep, within the constraints of the doubt principle. If the oscillating particle is localized, the momentum and therefore energy of the oscillator are distributed.

Problems

Show that the two everyman energy states of the uncomplicated harmonic oscillator, ${\psi }_{0}\left(x\right)$ and ${\psi }_{1}\left(x\right)$ from (Effigy), satisfy (Effigy).

proof

If the basis state free energy of a simple harmonic oscillator is 1.25 eV, what is the frequency of its motion?

When a quantum harmonic oscillator makes a transition from the $\left(n+1\right)$ state to the north land and emits a 450-nm photon, what is its frequency?

$6.662\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{14}\phantom{\rule{0.2em}{0ex}}\text{Hz}$

A particle with mass 0.030 kg oscillates back-and-forth on a spring with frequency four.0 Hz. At the equilibrium position, information technology has a speed of 0.60 m/due south. If the particle is in a state of definite free energy, find its energy quantum number.

$n\approx 2.037\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{30}$

Find the expectation value $〈{x}^{\text{ }2}〉$ of the square of the position for a quantum harmonic oscillator in the basis state. Annotation: ${\int }_{\text{−}\infty }^{+\infty }dx{x}^{\text{ }2}{e}^{\text{ }-a\text{ }{x}^{\text{ }2}}=\sqrt{\pi }{\left(2{a}^{\text{ }3\text{/}2}\right)}^{\text{ }-1}$ .

Make up one's mind the expectation value of the potential energy for a breakthrough harmonic oscillator in the ground state. Apply this to calculate the expectation value of the kinetic energy.

$〈x〉=0.5m{\omega }^{2}〈{x}^{\text{ }2}〉=\hslash \omega \text{/}4$ ; $〈K〉=〈E〉-〈U〉=\hslash \omega \text{/}4$

Verify that ${\psi }_{1}\left(x\right)$ given by (Figure) is a solution of Schrӧdinger's equation for the quantum harmonic oscillator.

A mass of 0.250 kg oscillates on a spring with the force abiding 110 North/yard. Calculate the ground energy level and the separation between the next free energy levels. Limited the results in joules and in electron-volts. Are quantum effects important?

campanellawisideeple.blogspot.com

Source: https://opentextbc.ca/universityphysicsv3openstax/chapter/the-quantum-harmonic-oscillator/

Consider Again the Ground State of the Harmonic Osillator. Find X^2

54 The Quantum Harmonic Oscillator

Learning Objectives

The Classic Harmonic Oscillator

The Quantum Harmonic Oscillator

Summary

Conceptual Questions

Problems

0 Response to "Consider Again the Ground State of the Harmonic Osillator. Find X^2"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel